Calculating Present and Future Value of Annuities
Oct 12, 2024 By Rick Novak
Are you looking for a better understanding of annuities and want to learn more about what they are and how to calculate current and future values? Then this blog post is just the thing for you.
A common financial tool that can provide consistent payments over an agreed-upon period, annuities have become increasingly popular in retirement planning.
In our introduction to calculating an annuity's present and future value, we'll explore why they are so vital in finance, providing insight into how these sums work – from their structure to predicting potential investment outcomes.
So understand that annuity calculations may be crucial when planning your long-term finances or investments!
Annuity Definition

An annuity is a fixed sum of money paid to an individual regularly, typically at specific intervals such as annually or monthly. Annuities can be used to provide income in retirement or for any other purpose.
Understanding Present Value vs. Future Value for Annuities

Present and future values are important when considering annuities. Annuities allow investors to receive a series of payments over time, usually regularly, such as annually or monthly.
The present value of an annuity is the current worth of an investment that pays a known series of payments in the future, whereas its future value is the amount to which this same investment will grow over time.
Understanding present and future values regarding annuities are important concepts that investors should understand before making investment decisions.
By evaluating annuities' present and future values, investors can make more informed investment decisions and plan their financial futures accordingly.
Two Types of Annuities
The two basic types of annuities are:
- Ordinary annuities.
- Due annuities.
An ordinary annuity is a series of payments that occur at the end of each period. Examples of ordinary annuities include bond payments or loan repayments.
On the other hand, annuities due require payments at the beginning of each period. Rent is one example of an annuity due. The formulas for calculating present and future value for both types of annuities will be discussed below.
Calculate the Future Values of an Ordinary Annuites
Calculate the future value of an ordinary annuity involves multiplying a cash flow the per period by a factor that considers both the interest rate and the number of payments.
The formula for calculate the future value of an ordinary annuity is as follows: FV = C x [(1 + i)^n - 1] / i, where
- C is the cash flow the per period,
- i is the interest rate,
- and n is the number of many periods.
For example, if you are making monthly payments on a loan at a 2% annual interest rate over 60 months, then your future value would be calculated as follows: FV = C x [(1 + 0.02/12)^60 - 1] / (0.02/12). The resulting value would tell you how much your total payments will be worth at the end of the loan period.
The future value of an annuity can also be used when making investments, such as a retirement savings plan.
Calculating an Ordinary Annuity's Present Value
The present values of an ordinary annuities (PVOrdinary Anuity) is the current time value of a series of fixed payments made in the future. This equation helps to determine how much money needs to be invested now to receive a given sum at regular intervals over a set number of periods while considering the interest rate for each period.
The formula for calculating PVOrdinary Annuity is C x [(1 - (1 + i)-n), where
- "C" represents the amount being paid each period,
- "i" is the periodic interest rate
- , and "n" is the total number of many periods.
In our example, we have a payment of $1000 per 6 months for 4 years. To calculate the present value of this annuity, we need to plug these numbers into the formula:
PVOrdinary Annuity = $1,000 × [(1 − (1 + 0.06)−8)]
= $6,097.82
If you invested $6,097.82 now, you would receive $8,000 after 4 years at a 6% interest rate per period. The amount of money invested now is lower than the future value because it takes into account the interest earned over time and its compounding effect.
By calculating an ordinary annuity, you can determine how much money needs to be invested now to receive a given sum at regular intervals over a set number of many periods.
Calculating the Future Value of an Annuity Due
The future value of an annuity due is calculated by multiplying the periodic payments (C) by a factor that takes into account the interest rate (i) and the number of periods (n). This factor is represented as [(1 + i)n - 1] × (1 + i), which can be simplified to i / (1 + i).
The formula for calculating the future value of an annuity due is thus FVAnnuity Due = C × [(1 + i)n - 1] × (1+i). By multiplying the periodic payments by this factor, we can determine how much money would accumulate after n periods if those payments were invested at a given interest rate.
For example, if you had $1,000 to invest each year for 10 years at a 5% interest rate, the future value of your investment would be calculated as follows:
FVAnnuity Due = $1,000 × [(1 + 0.05)10 - 1] × (1+0.05)
= $16,028.52.
In this example, the future value of your investment is $16,028.52 after 10 years. This figure includes the principal amount invested and the accumulated interest over time.
Calculating the Present Value of an Annuity Due
To calculate the present value of an annuity due, you will need the following information:
- The amount of each payment (C).
- The number of payments (n).
- The interest rate or discount rate (i).
Once you have all these pieces of information, you can use the formula:
PV Annuity Due = C × [(1 - (1 + i) -n)] × (1 + i).
For example, if you have an annuity due with 10 payments of $100 each, and a 5% interest rate, you would plug those numbers into the formula as follows:
PV Annuity Due = 100 × [(1−(1+0.05)−10) × (1+0.05)]
PV Annuity Due = 100 × [(1-(1.63127)) × (1.05)]
PV Annuity Due = 100 × 0.32371
PV Annuity Due = $32.37
This means that the present value of the annuity due is $32.37, which is lower than the future value of $1000 because you receive payments at the beginning rather than the end of a period and therefore have to pay an "interest penalty."
The lower present value should be considered when buying, selling, or trading annuities. Additionally, you can use the same formula to calculate the future value of an annuity due by replacing the present value in the equation with the desired future value and solving for C.
Doing so lets you determine how much each period payment should be to achieve a predetermined future value.
FAQs
Can you calculate the present value of an annuity?
Yes, you can calculate the present value of an annuity using the formula PV Annuity Due = C × [(1 - (1 + i) -n)] × (1 + i).
How do you find the present value and future value of an annuity?
To calculate the present value of an annuity, you will need to know the amount of each payment (C), the number of payments (n), and the interest rate or discount rate (i). You can then use the formula PV Annuity Due = C × [(1 - (1 + i) -n)] × (1 + i). To find the future value of an annuity, you can use the formula FVAnnuity Due = C × [(1 + i)n - 1] × (1+i).
What is the difference between a present and future value?
The present value of an annuity is the current time value of a series of fixed payments that are made in the future. The future value of an annuity is how much money would accumulate after n periods if those payments were invested at a given interest rate.
Conclusion
Annuities are an important part of retirement planning, and understanding how to calculate the present and future value of annuities can help you make more informed financial decisions. Following the formulas outlined in this blog post, you can accurately determine how much each period payment should be and how much your investment will grow over time.

Cash Flow Maximisation

InCharge Debt Solutions Review

Are Stocks With Low P/E Ratios Always Better?
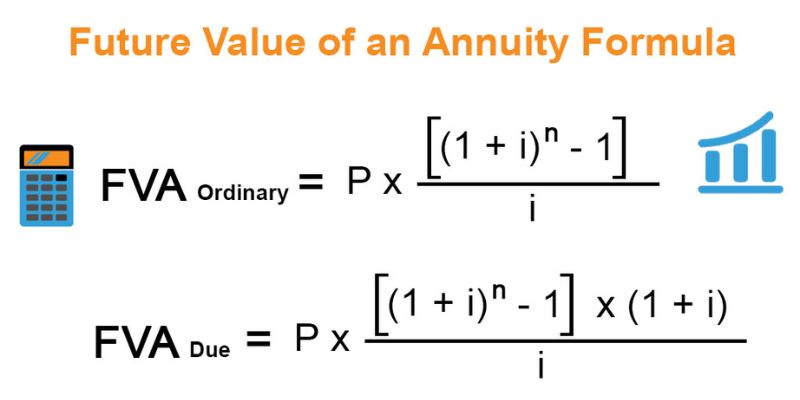
Calculating Present and Future Value of Annuities

Which Industries Have the Highest Inventory Turnover?

What Do You Need To Know About Cards?

What Is Cost-Volume-Profit (CVP) Analysis?

Deciphering Hedge Funds: Balancing Returns and Fees

What Are General Collateral Financing Trades?

